|
Reflection of
Electromagnetic Waves(电磁波的反射)
The impedance for electromagnetic waves is defined as the ratio
between the voltage and current waves,
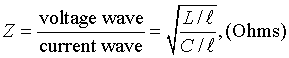
where
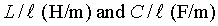
are inductance and capacitance
per unit length in medium. For example,the
inductance,capacitance, and impedance of a coaxial cable is
given by
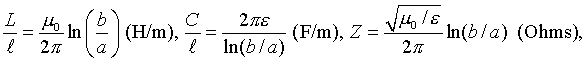
where a and b are the inner and
outer radii of the cable, and
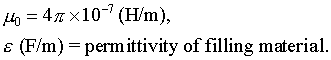
In free space, the impedance is
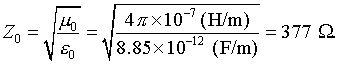
As mechanical waves are reflected
at an impedance discontinuity, so are electromagnetic waves. For
an incident voltage wave Vi , the reflected voltage wave at an
impedance discontinuity is
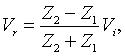
which should be compared with
that for mechanical displacement waves,
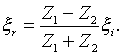
The difference is due to the fact
that displacement wave corresponds to current wave, while force
wave corresponds to voltage wave. In fact, the current waves
obey a formula similar to that of displacement wave,
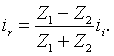
The first and second animation
shows,respectively, reflection of voltage and current waves at
the end of a 50 Ohm cable terminated with a 25 Ohm resistor. The
generator (10 V dc) is assumed to have the same resistance (50
Ohms) as the cable impedance to avoid further reflection. If the
generator has zero impedance, multiple reflections take place as
shown in the second animation. The case of zero generator
impedance is shown in the third and fourth animation.
The fifth animation shows reflection and transmission of
sinusoidal waves when the impedance of termianting load is one
quarter of the cable impedance.
Reflection can be avoided
entirely if a third medium having an impedance and length of
quarter wavelength is inserted. This well known quarter
wavelength impedance matching is shown in the last animation.
Note that there are no standing waves and all wave energy is
smoothly transferred to the cable 2.
V_g = 10 V, R_G = 50 Ohms, Z = 50 Ohms, R_L = 25 Ohms
Evolution of the voltage wave.
with(plots):
animate(5*Heaviside(t-x)-5/3*Heaviside(t+x),x=-10..1,t=-9..11,color=red,numpoints=300,frames=100,view=[-10..0,0..5]);
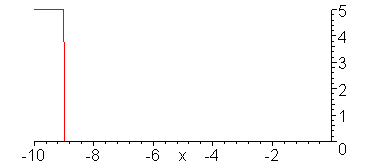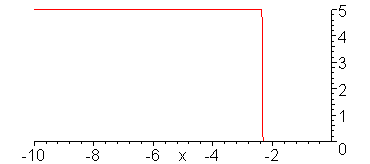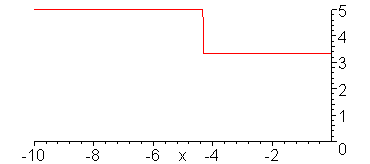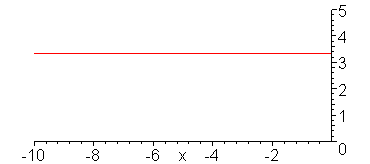
Evolution of the current wave.
animate(.1*Heaviside(t-x)+.1/3*Heaviside(t+x),x=-10..1,t=-9..11,color=red,numpoints=300,frames=100,view=[-10..0,0..0.2]);
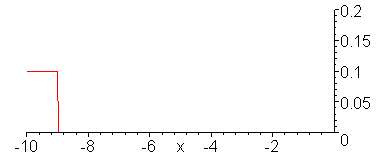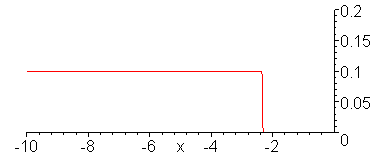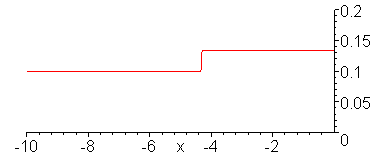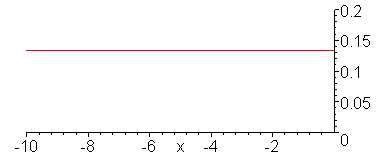
V_g = 10 V, R_G = 0, Z = 50 Ohms,
R_L = 25 Ohms
Voltage wave.
animate(10*Heaviside(t-x)-10/3*Heaviside(t+x)+10/3*Heaviside(t-x-10)-10/9*Heaviside(t+x-10)+10/9*Heaviside(t-x-20)-10/27*Heaviside(t+x-20)+10/27*Heaviside(t-x-30),x=-5..0,t=-6..30,color=red,numpoints=300,frames=200,view=[-5..0,0..10]);
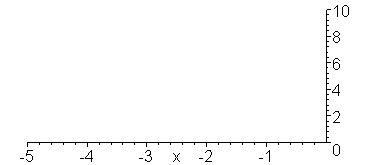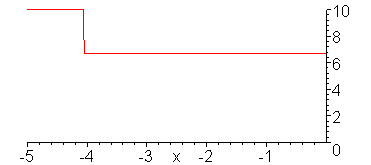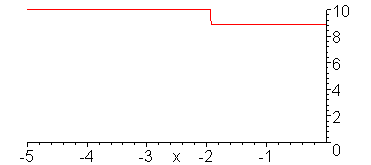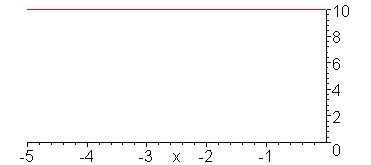
Current wave.
animate(.2*Heaviside(t-x)+.2/3*Heaviside(t+x)+.2/3*Heaviside(t-x-10)+.2/9*Heaviside(t+x-10)+.2/9*Heaviside(t-x-20)+.2/27*Heaviside(t+x-20)+.2/27*Heaviside(t-x-30),x=-5..0,t=-6..30,color=red,numpoints=300,frames=200,view=[-5..0,0..0.4]);
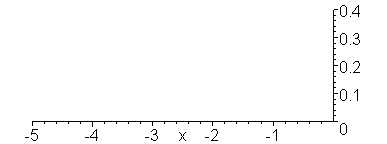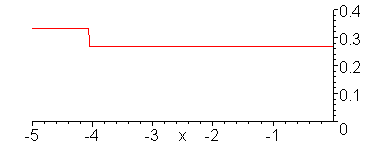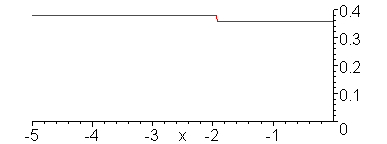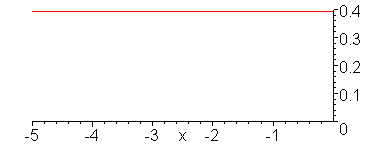
Reflection of sinusoidal voltage
wave when V_g = 1 V, Z_2/Z_1 = 1/4. Note formation of incomplete
standing in medium 1.
with(plots):
animate((sin(.1*t-x)-3/5*sin(x+.1*t))*Heaviside(-x)+2/5*sin(.1*t-4*x)*Heaviside(x),x=-10..5,t=0..62,frames=30,color=red,numpoints=300);
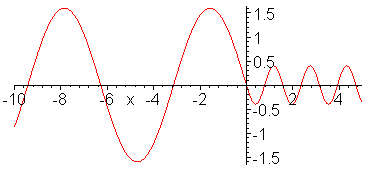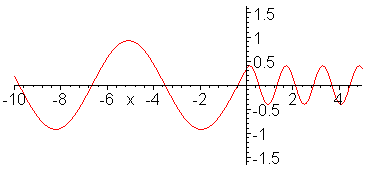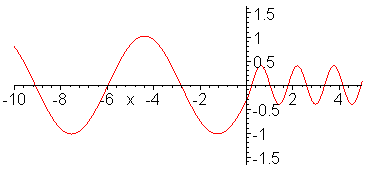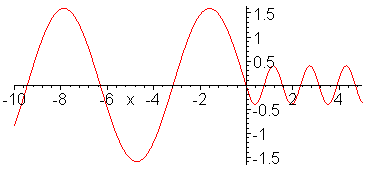
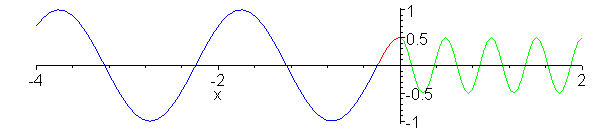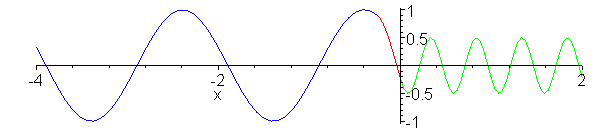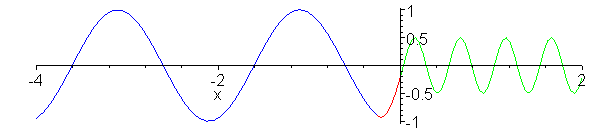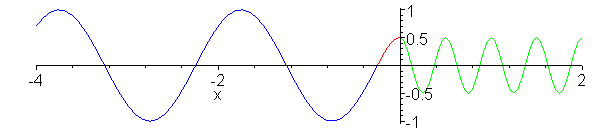
Impedance matching. Z_1 = 1, Z_2
= 1/4, Z_3 = 1/2. Inserted Z_3 medium (shown in red) is quarter
wavelength thick (or long). No reflection occurs and wave energy
is smoothly transfered to cable 2. Note the absence of standing
waves.
with(plots):
a:=animate(.75*(cos(2*Pi*.1*t-2*Pi*x)-1/3*cos(2*Pi*.1*t+2*Pi*x)),x=-0.25..0,t=0..20,color=red,frames=60):
b:=animate(cos(2*Pi*.1*t-2*Pi*x/2+Pi/4),x=-4..-0.25,t=0..20,color=blue,frames=60):
c:=animate(.5*cos(2*Pi*.1*t-4*Pi*x),x=0..2,t=0..20,color=green,frames=60):
display({a,b,c});
 |